An Introduction to Lagrangian Mechanics
How to go from (classical) particles to (quantum) fields.
The most fundamental task in physics is to calcutlate the equation of motion of an object. This describes how the main physical variables of the system, like position and velocity, evolve as a function of time. Once you know the equation of motion, you know all of the interesting dynamics, whether it be a ball at the park or a boson in a particle collider.
Traditionally, intro physics classes teach students how to do this using Newton’s laws. The recipe is fairly straightforward:
Write down all the forces that act on your object.
Take their vector sum and call the result the net force. Set this equal to the product of mass and acceleration. This is Newton’s second law F = ma.
Plug and chug to solve for the position and velocity. Usually both the force and acceleration are time-varying, so this step gives a differential equation to solve for the variables of interest.
This method has the wonderful advantage of being easily interpretable. In many cases, you can draw a diagram and label the forces with arrows. Because it’s very intuitive, this is what intro physics classes teach.
However, as we get into more advanced areas of physics like particle physics and general relativity, we very quickly lose the ability to just tally up all our forces and take vector sums. This is where we have to switch to a more sophisticated variant of mechanics: Lagrangian mechanics.
Lagrangian Mechanics
The foundation of Lagrangian mechanics is the principle of stationary action. This is the formalisation of a notion that most of us intuitively have: nature seems to take the path of least resistance.
To define this properly, first let’s define the action. Suppose we have a physical system where the coordinate x(t) describes the dynamics of interest over the time between t = T1 and t = T2. Then the action, S[x(t)], is a functional of the entire path x(t) in that time interval, and is given by the integral
The integrand L is called the Lagrangian, and is defined to be the the difference between the kinetic energy T and the potential energy V of the system
The action is therefore a number that you get by integrating the Lagrangian along a particular path x(t) of the system’s evolution.
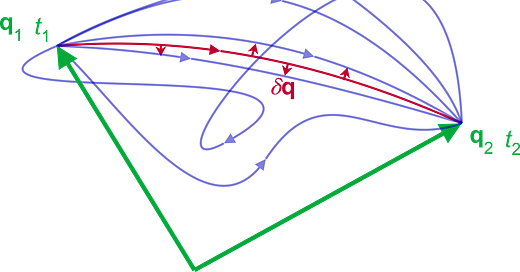
The principle of stationary action states that the path x(t) the system actually follows in nature is the one that makes the action stationary, i.e. makes it a minimum, maximum, or a saddle point.
Deriving the Euler-Lagrange Equations
Let’s be a bit more precise. The action is a functional and not a function so we have to be careful in what we mean by a stationary point. Instead of a normal function that has a stationary point at some fixed coordinate, a functional like action has a stationary point over an entire path x(t).
More formally, suppose the path that the system takes x(t) is perturbed by a small change so that x(t) → x(t) + εη(t). We have the condition that x(t) must begin at x(T1) and end at x(T2) so η(T1) = η(T2) = 0.
The first order variation in the action S as we tweak the path x(t) is
The principle of stationary action states that the x(t) we see in nature makes δS = 0. If you substitute in the definition of the action and go through taking the derivative of the integral, you end up getting that this condition requires the Euler-Lagrange Equations:
This is the Lagrangian equivalent of Newton’s Second Law.
The picture below shows this visually. The endpoints are (q1, t1), (q2, t2) and the purple lines represent some of the possible random paths between them. The path that nature actually takes, red, is the one which leaves the action unchanged for small changes δq.
Lagrange vs Newton: Mass On A Spring
To compare these two methods, let’s do a simple example with the physicist’s favourite system: the mass on a spring.
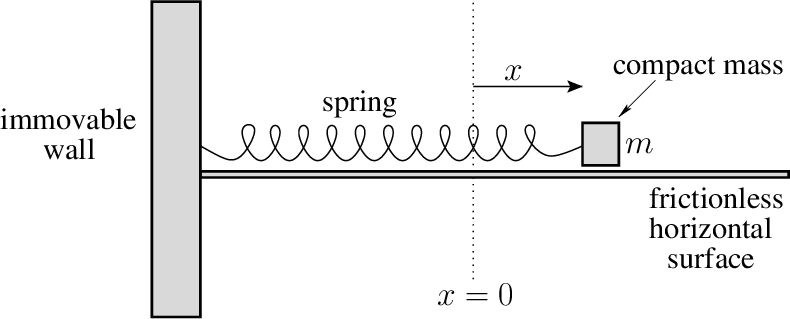
Let’s assume a mass m is sitting on a table and is connected to a spring with stiffness k. There is only horizontal motion so let’s define x to be the coordinate that tracks this motion, and let’s say x = 0 at the point where the block starts off at equilibrium. Finally, let’s say x is positive going to the right and negative to the left. See the diagram below:
Newtonian Picture:
First we consider the forces on the block. Let’s assume we displace the block by a small positive displacement x to the right from its equilibrium position. Then the spring will want to pull it back towards the starting point, and this force is given by F = -kx. The minus sign accounts for the spring pulling back to the starting point. For simplicity let’s say there is no friction so the spring force is the only force. Then Newton’s Second Law F = ma says
This equation — the simple harmonic oscillator — is ubiquitous throughout physics with a simple solution:
Where A and φ are constants that depend on initial conditions and ω0 is the frequency of oscillation which depends on the spring stiffness and mass m. So as you might intuitively expect, the mass just bobs back and forth around its equilibrium point.
Lagrangian Picture:
The Lagrangian is given by L = T-V. The kinetic energy is given by:
The potential energy comes from the spring — if you stretch the spring it wants to pull back and if you compress it it wants to push out. This is given by
You can derive this by using the fact that force is the negative gradient of potential energy together with F = -kx for a spring.
Putting these together we get the Lagrangian
Now putting this through the Euler-Lagrange equations we get
Which is the exact same equation we got from the Newtonian analysis!
From Particles to Fields
Ok so we showed that Lagrangian and Newtonian mechanics give the same thing, so why come up with an alternative when the first one works just fine?
One practical answer is that sometimes there are problems where you could technically do Newtonian mechanics but it is a pain, while Lagrangian mechanics is much easier. The double pendulum is the best example of this.
But a more fundamental answer comes when we revise our assumption that physics consists of only of rigid particles which move under forces. A crucial second ingredient for our description of the universe is that of fields. For our purposes, a field is simply a physical quantity that has a value at all points in space and time. Electric and magnetic fields are examples of this.
To motivate fields, let’s start from forces. Specifically, let’s consider two particles with electric charge q1 and q2. If these are separated by a distance r, the electric force of attraction (or repulsion) between them is given by:
Where ε_0 is a constant called the permittivity of free space. This law works beautifully. But it hides a puzzle: how does one charge “know” the other is there? There's no time delay in the formula. It seems like the force is instant — as if the two charges are reaching across space and tugging on each other. That goes against Einstein’s theory of relativity, which tells us that information can’t travel faster than light.
We can solve this using fields. In our example, the way to reconcile this problem is to introduce an electric field, E(x,y,z,t) (bold because it’s a vector quantity) that mediates the interaction between the two charges. Each particle creates its own electric field E that exists in all of space. Then, the total force particle 1 feels from particle 2 is simply the product of particle 2’s electric charge with particle 1’s electric field:
Now the interaction is local. Each charge responds only to the field at its own location. And the field itself spreads out through space, carrying changes at the speed of light.
So the force between particles is no longer a mysterious long-range handshake — it’s a consequence of something real in the space between them: the field.
If you run with this field formulation, you eventually get Maxwell’s equations, which describe exactly how electric and magnetic (B) fields evolve in space and time.
If you solve these equations, you find that disturbances in the fields travel at a finite speed: the speed of light. In fact, light itself is just a wave in the electric and magnetic fields.
So the picture becomes that particles interact by creating fields, and fields mediate the forces between them. Fields ensure that physics respects the constraints of relativity like causality and locality .
In fact in the modern physics picture, fields are arguably more fundamental than particles. In quantum field theory (QFT) for instance, fields are treated as fundamental and particles are just particular excitations of the fields — hence quantum field and not quantum particle theory.
Just like for particles, we are very interested in understanding the dynamics of fields. However in this case, you can’t just write the forces felt by the field and sum them up and use Newton’s second law.
To see why that doesn’t make sense, let’s consider a simple field — ripples on the surface of a pond. At each point in the pond, given by coordinates (x,y), there is a height of the water so our field is h(x,y,t). Suppose there is a ripple across the surface, which gives some pattern r(x,y,t).
Treating this ripple as a single particle and asking what is its position or acceleration isn’t well defined because the ripple doesn’t have a single position. It is defined all across the surface of the pond. There is no single coordinate (x,y,t) where the ripple “exists”.
In the same way, a field isn’t an object with a single location or trajectory. It’s a function defined over all of space and time. So instead of writing Newton’s second law for a single point mass, we need something more powerful: a way to describe how the entire field evolves.
Fields, Lagrangians, and The Higgs Boson
Well not to worry, because while fields do not have well defined single positions like particles, they do have well defined energies. That means you can write Lagrangians for them and do Lagrangian mechanics!
Let’s consider the simplest example from quantum field theory: the Klein–Gordon equation. This was the first attempt — made by Schrödinger — to describe electrons in a way that was consistent with both quantum mechanics and special relativity.
We’ll call the field we’re trying to model ψ. In the field theory picture, particles like electrons are no longer fundamental — instead, they’re seen as excitations of this underlying electron field ψ, whose dynamics we want to understand.
For simplicity, let’s assume we live in a one dimensional world with one spatial dimension x and time t. So ψ is a function of x and t only. Just like before, we build the Lagrangian from kinetic and potential energy — but now these are energy densities (energy per unit length), since our system is continuous across space.
The kinetic term, in analogy to the previous mass on a spring case, is given by the time derivative of ψ:
We have switched notation here where ∂_t ψ = dψ/dt. This will be much more useful when we generalise to multiple dimensions.
The potential energy term includes a term proportional to ψ^2 similar to the mass on a spring that becomes higher the further the field is away from its equilibrium 0 value. However, it also has an extra term that couples the value of ψ at different positions in space together, given by the spatial derivative ∂_x ψ:
One way to think about this spatial derivative term is that is if the spatial derivative of the field is really high at a point, then we are stretching the field out while it would much rather be in its flat lower energy state with zero slope. Think of playing with a stretchy sheet. You can stretch it but it’d much rather be flat.
Now we combine these to get our total Lagrangian density L = T - V:
Where m is the mass of the particles that this field creates. Note that we’re working in “natural” units, where fundamental constants like c = 1.
Now we put this through the Euler-Lagrange Equations. Here, we have to use the more general version which incorporates not just time but also spatial derivatives:1
Plugging and chugging through this, you obtain the Klein-Gordon Equation in a 1+1 dimensional spacetime:
Or if you prefer in SI units
A couple of things to note:
If the spatial variation term ∂_x ψ = 0, then we obtain exactly the equation of a mass on a spring from before! Each point of the field basically behaves as an uncoupled mass on a spring system. The spatial variation is what couples them and gives interesting excitations.
This equation is inherently compatible with Einstein’s requirements from relativity. It is what we call Lorentz invariant.2 This shows how fields naturally impose restrictions like causality and locality that arise from relativity.
Now as it turns out, the Klein-Gordon equation doesn’t actually model electrons due to a subtle quantum mechanical effect called spin, but it does model particles which don’t have any spin, like the infamous Higgs boson that gives other particles mass.
You can get much more complicated than this. For example, you can derive all of Maxwell’s equations from a Lagrangian although doing so requires knowing some basics of special relativity like Einstein index notation and how to use 4-vectors.
So we see that while Lagrangian mechanics is technically equivalent to Newtonian mechanics, it ends up having a far broader scope. The reason for this seems to be simply that nature rather elegantly chooses to follow the principle of stationary action. Why this is true is an open question, but we should be grateful that it is because it lets us come up with a fabulously elegant framework to describe physics from a ball bouncing on a slinky to the particles that make up the very essence of the universe.
Note: you can derive this using exactly the same analysis as above where the first order action variation has to go to 0 but now let η vary in x in addition to t.
Mathematically, if you transform your coordinate system in the way that relativity says (undergo a so-called Lorentz boost) that takes the coordinates (x, t) to some new coordinate system (x’, t’), the Klein-Gordon equation will look exactly the same.