Picture yourself racing alongside a beam of light, matching its incredible speed of 300 million meters per second. What would you see? Would the light appear frozen beside you, like a car keeping pace on the highway? This is the question that haunted a young Albert Einstein and ultimately led him to one of the most beautiful theories in all of physics — special relativity.
A Luminous Mystery
The crowning achievement of 19th century physics was the complete understanding of electromagnetism. Through the work of pioneers like Ampère, Gauss, and Maxwell, we arrived at a set of equations that gave us a complete description of electricity and magnetism. One of the most beautiful discoveries from this theory is that electric (E) and magnetic (B) fields can travel in waves:

You know these electromagnetic waves as light.
Typically, a wave needs something to travel through. Sound travels through air, ripples travel across water in a pond. So naturally people wondered: what is the medium that light travels through? Can we make a measurement of its properties?
One way to probe this mysterious medium — dubbed rather romantically as the “luminiferous ether” — is to try measure the speed of light. To motivate this, let’s think about a wave jiggling on a fixed string:
The weight on the left applies some tension and keeps the string fixed on that end, while the oscillator on the right jiggles the rope up and down and causes waves to travel across it. Something simple to ask is how does the wave change if I put more weight on the pulley and increase the tension on the rope. You can show that the velocity of the wave is proportional to the square root of the tension. So by measuring the speed of the wave, you can measure the tension in the rope.
Similarly, physicists at the turn of the century mulled over ways to use the speed of light to probe the ether. Two physicists, Michelson and Morley, had a very simple idea to test this out. They reasoned that the speed of light on Earth should change as the direction of the Earth changes relative to the ether. It’s just like if you’re swimming in a river you will swim faster downstream than upstream.

The Michelson-Morley experiment famously found no difference in the speed of light in different directions (see, null results are good for science!). This meant one of two things:
The Earth was somehow magically always stationary relative to the ether, i.e. they are both always moving in the same speed and direction.
There is no ether, and the speed of light is just always the same in all directions.
The first implies some very privileged role for the Earth, as if the ether is oriented throughout the universe just to match up with us, which seems too good to be true. The second option is the more plausible yet mysterious one, and it was the one Einstein was mulling over in the early 1900s.
It’s All Relative
Grappling with this tension is what led Einstein to special relativity (SR). He decided to just accept outcome 2 of Michelson-Morley. In the paper where he introduced SR — On the Electrodynamics of Moving Bodies — he forms the theory based on two foundational postulates:
The laws of physics are the same for all inertial observers
The speed of light is the same for all observers
What is an inertial observer? In the simplest terms, an inertial observer is an observer who is traveling at a constant velocity, i.e. not accelerating. Recall this means that not only is the magnitude of the velocity constant, but so is the direction. So an inertial observer is moving at a constant speed in one direction. Note that being at rest is a special case of being at constant velocity.
An observer may also be called a frame of reference, so an inertial observer and inertial frame of reference are the same thing.1
With that caveat aside, postulate one is eminently reasonable. The laws of physics wouldn’t be particularly useful if they were different for different people. Postulate two is the mysterious one from Michelson-Morley that we just have to accept for now.
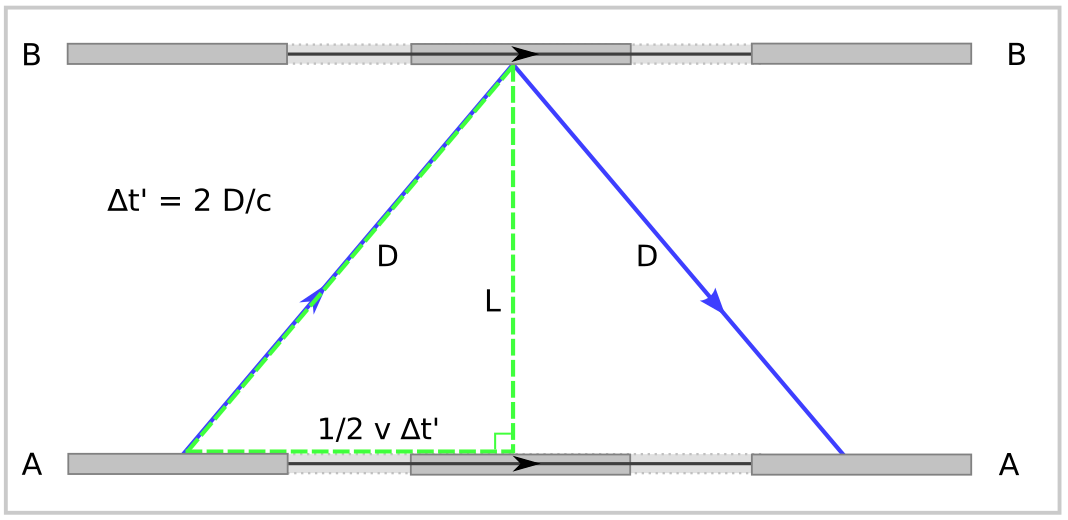
To explore the consequences of these two, let’s do a simple experiment. Suppose Alice is in a rocket ship traveling at a speed v. Note that for Alice to be an inertial observer, v is constant in time. Inside the rocket, she shines a light at the roof and the light rays travel up the height of the rocket — let’s call this L — and then they bounce off the roof and come back down. See the picture below:
The time that Alice measures for the light ray to come back to her is given by
Nothing fancy here — just an application of distance = speed x time.
Now suppose Bob is sitting outside and watching Alice zoom past him at speed v. He can also see Alice switching on her light and does the same experiment to measure the time it takes for the photons to go up and come back down. What does he measure?
What Bob sees is shown in the diagram below:
As Alice zooms past Bob, he sees the light go not only up, but forward also. The time that Bob measures, ∆t_B, is given by:
The total distance traveled by the ship in this time interval is given by speed x time so the bottom of the triangle has a length of v ∆t_B. With the green right-angled triangle, we can use Pythagoras’ theorem to express D in terms of the other variables we know:
Plugging this into the previous equation for ∆t’ gives
We can substitute in for L in terms of ∆t that we calculated from Alice’s measurement:
Now if you play around with this you get
So what does this mean? Well ∆t_B does not equal ∆t_A — Bob measures a different time than Alice!
Okay so who is right? It turns out they are both correct. Through this simple thought experiment, we immediately start seeing the weirdness that emerges from the two postulates. Just to recap, postulate 1 meant that we used the same physical equations for both observers, and postulate 2 meant that the factor c is the same in both equations.
What we just derived is a phenomenon called time dilation. It’s the very real effect that moving clocks run slower and in our example the light bouncing up and down is the clock. If Alice measures a time of 5 seconds for the light to go up and come down, Bob will always measure a time greater than 5 seconds. Only if Alice and Bob aren’t moving relative to each other — e.g. if Bob is in the rocket with Alice and they are in the same frame of reference — will both measure the same time.
Note that this effect depends on the ratio of v to c. The reason why we don’t see these effects in everyday life is because we never remotely approach the speed of light, i.e. v << c, so the denominator in the formula is basically 1 and the two time intervals are the same within measurement error of whatever clock you use.
Time dilation has a spatial counterpart called length contraction: to an observer, a moving object appears shorter along the direction of its motion than it does in its own rest frame. In our example, if Alice held a stick pointed in the direction of travel which she measured to be of length L_A , Bob would observe that stick to be a length
Just for fun, here’s a picture of what a basketball would look like if it were traveling near the speed of light and became length contracted
You may have noticed this factor √(1-v^2/c^2) popping up in both time dilation and length contraction formulas. This factor — the Lorentz factor — is so common in relativity that it gets its own symbol:
You should convince yourself that for any value of 0 < v < c, γ >= 1.
Relativity in Action: Muons in the Sky
Time dilation sounds like an insane thing, but we do unmistakably see it in the real world. One of the best known examples of this is muons in the atmosphere.
Muons are a fundamental particle, kind of like a heavier electron. They are produced when cosmic rays from space hit particles in the atmosphere. These collisions produce all sorts of intermediate particles many of which eventually decay into muons. We can detect these muons pretty easily at the surface because they are very abundant.
Muons are also unstable and decay very quickly into electrons with a mean lifetime of 2.2 µs (0.000002 s). When they are produced, they usually travel at speeds very close to the speed of light, let’s say something like 0.999c. Based on this, we can estimate the distance a muon should travel before it decays:
So the muons will travel on average 659 m before decaying, but they are created at altitudes of close to 15,000 m, about 23 times the average decay length. How can we possibly detect a significant number of muons on the surface of the earth? Shouldn’t they all have decayed into electrons?
Here, time dilation comes to our rescue, and this situation is very analogous to Bob and Alice. In this case the muon is Alice and the external observer is Bob. If the muon had a clock, it would see 2.2 µs having passed, but for us on the earth we would measure a larger time given by our previous formula:
So the distance we observe the muon traveling before it dies is
Which is basically the height of the atmosphere!
This might sound like a bit of a scam, so let’s look at things from the muon’s perspective to show that everything is consistent. In the muon’s own frame of reference, it sits still and instead sees the Earth coming up to it at a speed of 0.999c.
In the muon frame, it will only be alive for 2.2 µs, and in that time the Earth can only come up a distance of d = 2.2 µs x 0.999c = 659m. How can the muon and surface ever reach each other? Surely it’s not possible that from our external perspective that the muon hits the surface but from its own perspective the muon does not — physics has to be the same for all observers!!
Well here, it’s length contraction that saves us. The muon sees the distance to the surface of the Earth not as 14.5 km, but as the length contracted version:
Voila! There is no inconsistency. All observers can agree that the muon does indeed reach the surface of the Earth.
Light Cones, Spacetime Intervals, and Lorentz Transformations
Hopefully those initial examples convinced you that once the speed of light is fixed, time and space start doing funky things. Now, we can take a little bit more of a structured approach to exploring the consequences of these postulates.
Suppose we live in a universe with a spacetime of one spatial and one time dimension and we are sitting at the origin with coordinates (x, t) = (0, 0). At t=0 we fire off a flash of light in the +x and -x directions. Since the speed of light is constant c in all directions and for all observers, both rays of light will travel at the same speed. The ray moving in the +x direction will have a position x = ct after a time t. Similarly, the ray moving in the -x direction will have a position x = -ct. At a particular time t, the two points the light rays are at are x = +/- ct or more concisely:
The picture below — called a spacetime diagram — shows this:

Here both dotted lines together are the equation c^2 t^2 = x^2. Both individual lines have slope 1/c (since time is on the y axis). If you travel slower than c, your line will have a greater slope than the dotted one. In our universe, all matter with mass must travel slower than c, and massless matter (like photons of light) can travel only at c.
This means that no matter what you do, if you are sitting at the origin you can only ever hope to reach/communicate with those regions of the diagram that are shaded in grey. To communicate with any other region would require faster than light communication, which is impossible. The grey area, which is the set of all spacetime causally connected to you at the origin, is called the light cone. The part with t > 0 is the future light cone, and the part with t < 0 is called the past light cone.
Why a cone? Well suppose we went from 1+1 dimension spacetime to a 2+1 dimension with x and y. In that case the picture would be the same just rotated around so your two light lines would define a cone:

Here at each time t, instead of x^2 = c^2 t^2 you have that x^2 + y^2 = c^2 t^2. Of course you will note our universe has 3 spatial dimensions x, y, and z. The light cone applies in 3+1 dimensions also it’s just hard to draw. The cone is nevertheless defined in the same way:
(Now you know what Sam Altman is getting at when he talks about AI and the “light cone” of future value.)
Since the speed of light is constant, all observers must agree on which events can be causally connected. If observer A sees events X and Y as causally connected, so must observer B. In our muon example, the external observer saw the event “muon is created in the atmosphere” and “muon hits the surface” as causally connected, and as we confirmed, so would an observer traveling in the muon’s own frame of reference. Since observers must agree on the light cone, defined by the above quadratic equation, they must also agree on the value of the spacetime interval:
On the light cone itself, ∆s^2 = 0. In the causal part of the light cone, ∆s^2 > 0 and in the non causal part outside the light cone ∆s^2 < 0. The causal region is called timelike and the non-causal region is called spacelike. The light cone itself is, unsurprisingly, called lightlike.2
The concrete mathematical statement for “all observers must agree with each other on causally connected events” is that all observers must observe the same spacetime interval. To be precise, suppose an event has coordinates (x, y, z, t) in my frame of reference and suppose it has coordinates (X, Y, Z, T) in yours. Then for both of us:
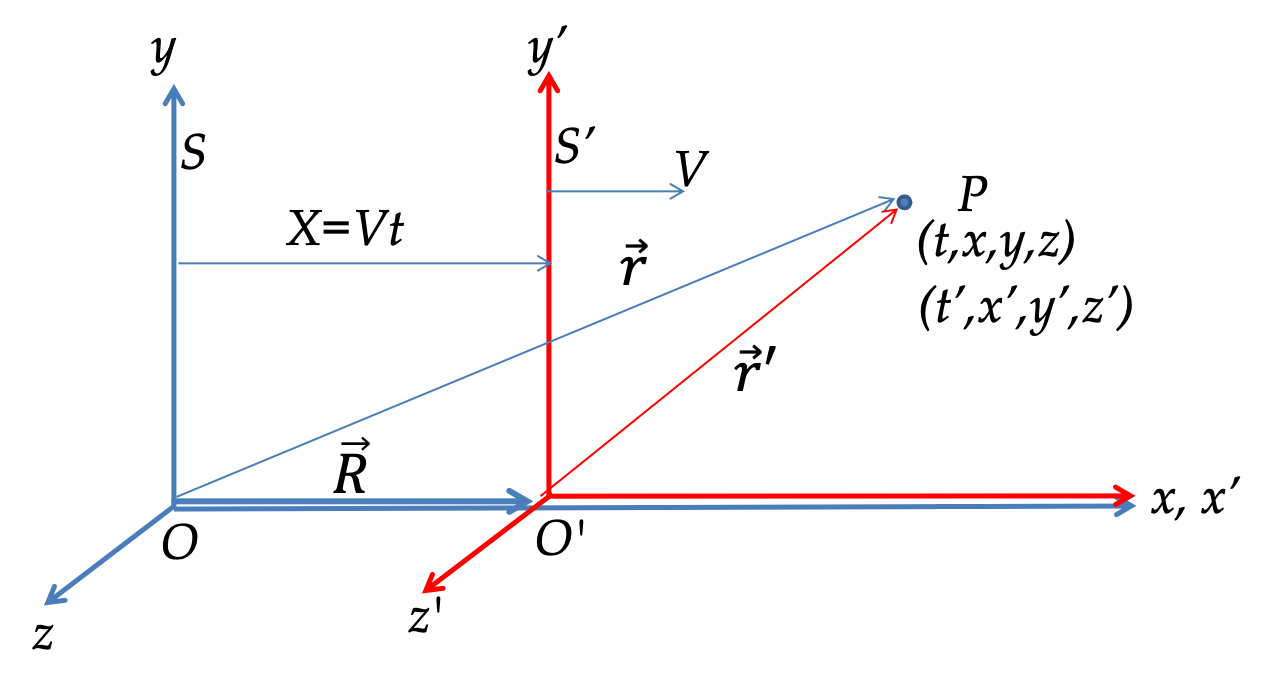
One question you can ask is how would you convert mathematically from my coordinates to yours? Let’s first consider this in a classical universe without any relativity. Take the example of two frames in the image below:
The red frame, with coordinates x’, y’, z’, t’ is moving at a constant speed V relative to the blue frame with coordinates x, y, z, t. The motion is only in the x direction, so it’s not too hard to see that y’ = y and z = z’. Of course in this classical world t = t’. The only change between the frames is is that x’ = x - Vt (prove this to yourself). These formulas are known as Galilean transformations, after Galileo. One can show that Galilean transformations leave the Euclidean norm x^2 + y^2 + z^2 unchanged — i.e. both observers will agree on lengths and distances of things.
However as we showed, when we’re dealing with relativity, space and time get mixed, and the quantity that must be preserved for both frames is the spacetime interval ∆s^2. Running with this requirement, you can show that the actual relativity-consistent way to transform between frames is given by Lorentz transformations:
Where γ is the Lorentz factor defined above. Note how now time is not the same across both frames and both space and time mix into each other — one person’s time (t’) is a function of the other person’s space (x) and time (t). Also you can show yourself that if v << c, the Lorentz transformations reduce to the Galilean ones.
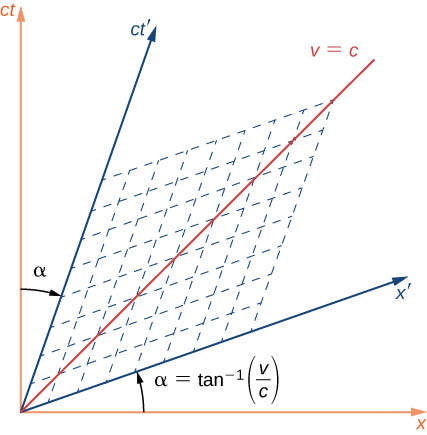
What do Lorentz transformations look like pictorially? Let’s go back to one space and one time dimension for visualisation purposes. In the picture below, orange represents a stationary reference frame, while dark blue is moving at a velocity v relative to orange. The y axis is time and the x axis is space:
Unlike a Galilean transformation, which simply moves the axes relative to each other, a Lorentz transformation actually “squeezes” the axes closer together. The angle of squeezing depends on the speed v. If you boost into a frame that is traveling at the speed of light, the axes collapse onto the red line in the middle, which corresponds to v = c. At that point, space and time literally become one and indistinguishable.
Relativity of Simultaneity
Let’s finish our foray into SR with a look at one of its most counterintuitive results: relativity of simultaneity. Look at the spacetime diagram below, which shows a frame x’, t’ Lorentz transformed relative to a frame x, t. Let A and B be two random events.
In the unprimed frame, A and B happen at the same time — they are both on the same blue gridline which corresponds to the same value of time on the black time axis. In the primed frame however, which uses the skewed red axes, A and B are not on the same time gridlines anymore. A is on the dotted green line and B is on the dotted blue line. That means while the unprimed frame sees A and B happening simultaneously, the primed frame does not!
To make this more palatable, suppose our event A was at the origin. If another event B happens at the same time, then B will be somewhere on the x axis on the spacetime diagram. As we saw in the light cone diagram above, this puts it in the non-causal region for A. If A and B happen at the same time, there is no way they can be causally connected because nothing can travel fast enough to convey information between them. Because they’re outside each other’s light cones, there is no absolute temporal order between them. Different inertial observers (i.e. observers in different frames) can disagree on which one happened first, and that disagreement does not contradict causality.
So we see that by accepting the speed of light as fundamental and unchanging leads to a complete overhaul of our understanding of space and time. In this article we went over some of the most basic new concepts, like time dilation and length contraction and how space and time truly blend into one spacetime. There are so many other profound effects we didn’t have time for, such as mass-energy equivalence — the infamous E = mc^2 — but those require some basic familiarity with SR. If there is interest I may do a part two in the future where we explore the dynamical consequences of holding the speed of light fixed.
Special Relativity doesn’t have anything to say about non-inertial observers, for that we have to go to General Relativity which is much more complicated.
You may see the spacetime interval shown instead as ∆s^2 = c^2 t^2 - x^2 - y^2 - z^2, i.e. the negative of what I’ve shown here. That is also a perfectly valid convention, and the one I personally prefer for reasons that would make this article too long. The convention in the main text is called the East Coast metric, while the convention in the footnote is called the West coast metric. If you use the + - - - convention instead, the definitions for timelike and spacelike get flipped — i.e. timelike becomes a positive spacetime interval instead of a negative one.